Graph IDE ► Graphs ► Non-Linear Graphs
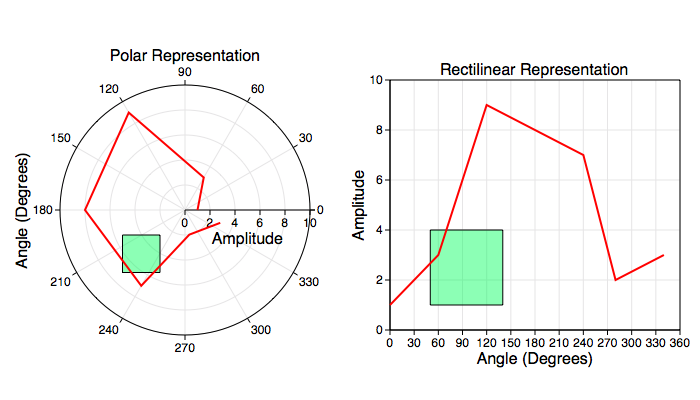
Non-Linear Graphs are graphs whose dimensions are not represented by uniformly spaced straight lines. For example, the polar graph shown here:

is considered non-linear while the rectilinear graph on the right is not. There are two graphics on each of those graphs, a green rectangle and a red sequence of line segments (a curve). The curve points are described in the circular and radial grid coordinate lines (namely {θ, r}) while the rectangle, which is a graphic-oriented graphic, is described in mapped rectilinear coordinates (namely {x, y}). The relationship is: r = sqrt(x x + y y) and θ = atan(y/x). The {θ, r} coordinate is called the domain space, while the {x, y} coordinate is called the range space.
So that the green rectangle has origin at point {-5, -5} and size {3, 3} for the left (polar) graph and origin at point {50, 1} and size {90, 3} for the right (rectilinear) graph. This is in contrast to the points that define the red curve. For both graphs the red curve has the same point values:
| θ (Degrees) | Amplitude |
| 0 | 1 |
| 60 | 3 |
| 120 | 9 |
| 180 | 8 |
| 240 | 7 |
| 280 | 2 |
| 340 | 3 |
That is because the curve is defined in the domain space of each graph, while the rectangle is defined in the range space of the graph. For general non-linear graphs there are three different representations (spaces) to be aware of:
| Representation Name | Description |
| Domain | This is the coordinate system as shown by the graph's grid lines and curves. |
| Range | This is the coordinate system after the non-linear mapping takes place and is a linear coordinate system. For example: xp = log(x). |
| Rectilinear | This is a secondary representation of either the domain or range representation. For polar coordinates this is another representation of the domain space, for log coordinates this is the range space. |
The only coordinate system where the three representations described above are unique is the log-r polar graph. The only one where they are the same (and hence only the Domain Representation is considered) is the normal Linear Axis graph.
The important part of non-linear graphs is to keep the representations in your mind while working with the graph, and which representation corresponds to which graphic. When dealing with multiple y-axis or x-axis graphs with linear and nonlinear axis this issue needs to be well thought out because one area on the graph can have many coordinate systems and spaces.