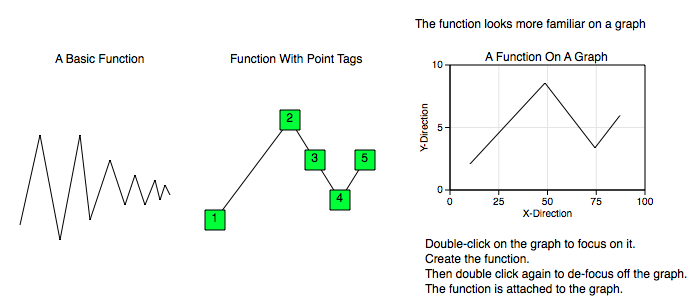
Graph IDE ► Data Graphics ► Function
a.k.a.: Curve or Line Graph
A function is a sequence of points connected by line segments. The x-values of the points increase as the sequence index increases. The figures below show examples of functions.

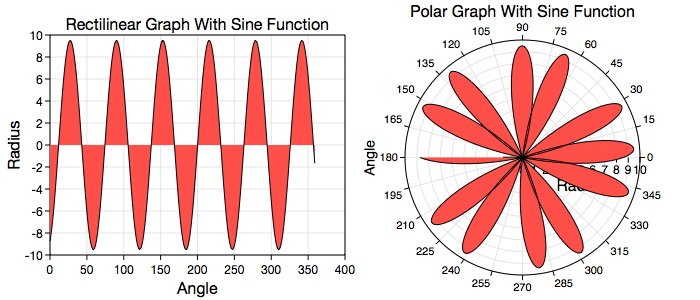
All Data Graphics, including this function graphic, transform according to the coordinates of the graph it is on. So, for example, the following graphs show the same exact function graphic (and same x and y point data) but on two different coordinate types. In the polar graph, the radius is mapped with an absolute value function. For additional information consult the Non-Linear Graphs section.
Some standard operations are itemized below.
Data Editor
The Data Editor for the Function is shown below.
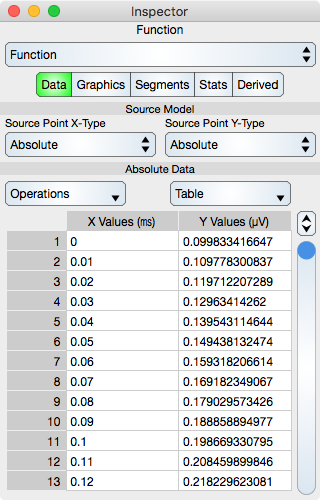
Source Model
Source Model transforms the original data to a new data set (called the range). Other models (for example, Programming Function) transform the original data directly, but Source Model takes the original data and transforms it. Once a source model is defined then user operations are on the range of the source model transformation.
The main reason to use a Source Model is when the data can not be computed directly. This happens for error bars and cumulative area graphs where the data is relative to a previous or next function graphic.
Source Point X-Type : Defines the built in type which is Absolute, Relative To Previous, or Relative to Next. Absolute means no transformation and is the default, Relative To Previous means to interpret the data as values relative to the previous graphic, which must be a Function graphic. Relative To Next means to interpret the data as values relative to the next graphic, which must be a Function graphic. The next or previous graphic is that graphic in the Layer sequence of graphics. When changing the source model you are given the opportunity to convert the original data so that it represents the new Source Model type instead of the old type. For example, if data is in absolute coordinates then converting the data will alter that data to values relative to the related graphic.
Source Point Y-Type : Same as Source Point X-Type except in the Y direction.
Table
Operations : Select this to perform common sequence operations upon the data. The most important sequence operation is Sort X-Ascending because the table data should always be x-ascending.
Generic table controls are described in the Tables section.
The rows represent vertex values. While in Atomic mode, the cell represents a point (x and y value) and while in component mode the cell represents either a x or y value. Hence, in atomic mode there is one column while in component mode there are two columns.
If points are imported into the table or edited and that operation does not produce x-ascending data then the table should be resorted using the Operations control, i.e.: x-ascending is not enforced and needs to be done explicitly.
X-ascending data is a convention that helps with optimization. It is also required to meet the definition of the Function graphic.
Graphics Editor
The Graphics Editor for the Function is shown below.
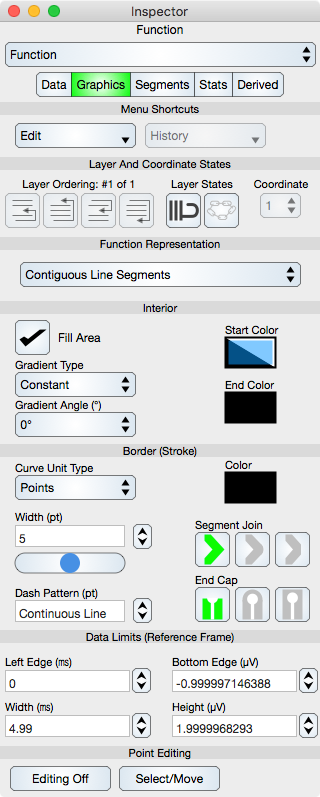
Common Controls
Controls common to all graphics are described in the Graphics section.
Coordinate : When the function resides on a Multiple Coordinate Graph then the coordinate control is used to define which coordinate it resides on.
Function Representation
Representation Type : One of the following: (a) Contiguous Line Segments: The normal line graph representing a continuous function, (b) Disconnected Y-Constant Segments: Signifies that the data is discrete and non-interpolated or (c) Connected Y-Constant Segments: A box function representation also used for histograms. In the case of (b) and (c) the Y-Constant Segments are centered about the x-value of the data and the x-length are from the midpoint between adjacent points while the y-value is that of the data for that point.
Point Editing
Editing Off/On : Places the graphic into or out of edit mode. While in edit mode the vertices are shown by indicators and can be adjusted using mouse or touch events. Double-clicking the graphic also toggles this edit mode.
Select/Move or Add/Delete : Select/Move mode permits the vertex editing to select and move those locations while Add/Delete mode will delete a vertex if it is hit or add a vertex if a Function segment is hit. This can also be accomplished using the shift key if available.
Segments Editor
The Segments Editor for the Function is shown below.
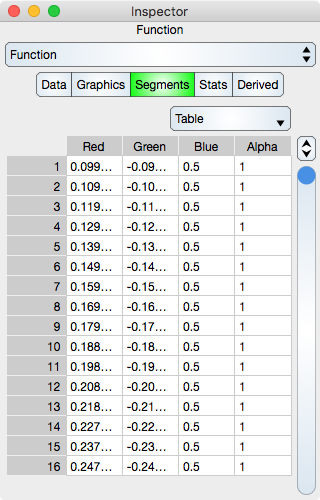
Segments are the line segments between adjacent points. See Sequence Colors for additional information.
Table
Table controls are described in the Tables section.
The rows represent segment color values. While in Atomic mode, the cell represents a rgba value and while in component mode the cell represents either single r, g, b and a. Hence, in atomic mode there is one column while in component mode there are four columns.
Note that if the Data sequence is resorted then the Segments sequence will not be resorted.
Stats Editor
The Stats Editor provides basic statistics for the Function and is shown below.
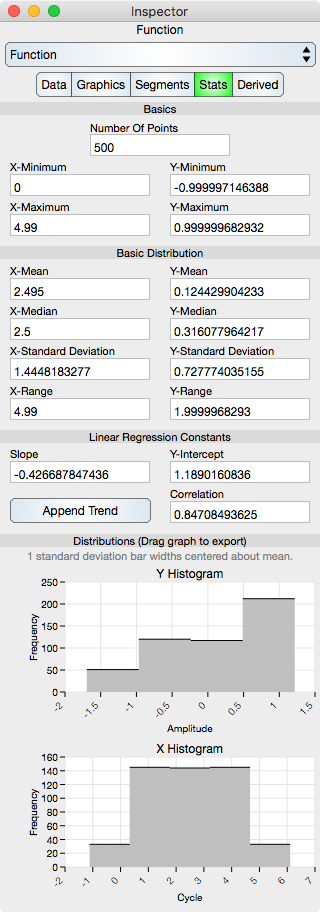
Basics
Number Of Points : Shows the number of points in the Function.
X-Minimum : x-minimum value of all the data points. Since the data points should be x-ascending, the x-minimum is the x-value of the first data point in the sequence.
Y-Minimum : y-minimum value of all the data points.
X-Maximum : x-maximum value of all the data points. Since the data points should be x-ascending, the x-maximum is the x-value of the last data point in the sequence.
Y-Maximum : y-maximum value of all the data points.
Basic Distribution
The basic distribution is shown separately for the x-dimension and the y-dimension. For a function, the y-distribution is the important distribution.
Mean : Shows the mean of the data.
Median : Shows the median of the data.
Standard Deviation : Shows the standard deviation of the data.
Range : Shows the range of the data (maximum - minimum).
Linear Regression Constants
Note that linear regression may also be referred to as line fit.
Slope : Shows the slope of the linear regression.
Y-Intercept : Shows the y-intercept of the linear regression.
Correlation : Shows the correlation constant of the linear regression.
Append Trend : Places a new trend line over the function. The trend is a least squares fit and each x-value of the function is also on the trend. Thus if the function is on a non-linear graph then the trend will map as well and not look like a linear fit on page view coordinates.
Distributions
Y Histogram : Shows the y-histogram of the data. This graph can be dragged onto the Graphic View.
X Histogram : Shows the x-histogram of the data. This graph can be dragged onto the Graphic View.
Derived Editor
The Derived Editor for the Function is shown below.
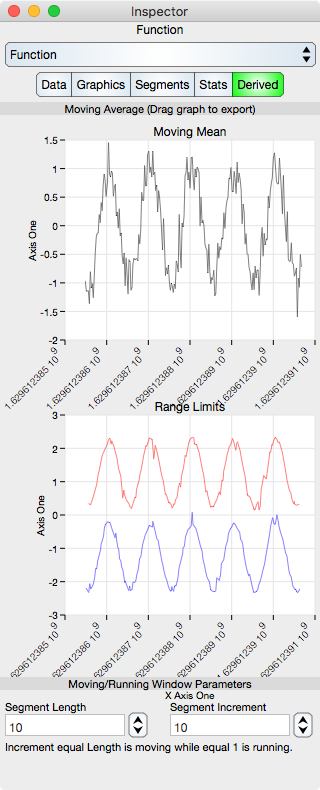
Derived output can be anything, but in this current implementation it is limited to moving average and range limit graphs. The Moving Average smooths out the function while the Range Limits show the minimum and maximum y-value within a bin of the moving average.
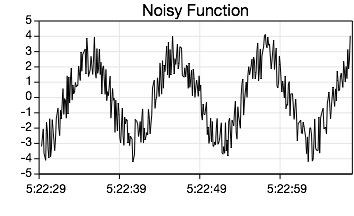
Consider the following noisy function:
Running Mean Graph : Shows the running mean of the data. When the segment increment is not 1 then this shows the Moving Average of the data. If the segment length and increment is one then the Running Mean Graph is the Identity.
Range Limits : Shows the minimum and maximum values within a bin defined by the Segment Length. The minimum is the blue curve and the maximum is the red curve.
The graphs can be dragged to the main document graphic view and then the derived curves can be copied and pasted to the graph's data layer so that the derived curves can overlay the original data. While the Derived values on the inspector are recomputed when the data changes, any pasted result is not.
As a side note, in this example notice how the derived graphs are on a rectilinear graph while the Noisy Function curve is on a Gregorian graph. When the curves are pasted onto the target coordinate then its x-values (representing seconds from 1970) are remapped to the Gregorian x-unit.
Segment Length : Defines the number of points that are used to compute the mean of the derived value. If 1 then the mean is the data itself. This value should be set great enough to span several values of noise while small enough to be within about 5 percent of the data variation.
Segment Increment : Defines the increment of the bin window. When 1 then the computation is a running mean and when equal to the segment length then the average is considered a moving mean. The main reason to set this greater than 1 is to reduce the number of points in the derived computation.